La revolución cuántica

Escrito por Alberto Casas y publicado por Penguin Random House dentro de la colección Sine qua non en el 2022.

Efectivamente, no había oído hablar del autor, pero le eché un vistazo a la parte interior de la portada y viendo el resumen que hacen de su cv, no tuve más remedio que comprármelo y echarle un vistazo. Y tengo que decir que, en mi opinión, ha merecido la pena.

Es doctor en física teórica y profesor de investigación del CSIC, ha trabajado en el CERN, en la universidad de Oxford, en la de California.... en fin, que de física cuántica debe saber algo como para poder explicar un poco el asunto a los no profesionales.

Nos habla y nos explica (dentro de lo que se puede explicar sin entrar en matemáticas avanzadas) todos los tópicos de la mecánica cuántica: la superposición, el gato de Schrödinger, el principio de incertidumbre, el efecto túnel, el entrelazamiento cuántico, la teoría de los muchos mundos, la teleportación, los bits y los qbits, la criptografía y la computación cuánticas y además deja un último capítulo para hablar de los límites de la física cuántica.

El libro prácticamente comienza con la hipótesis de Planck de que la energía de la luz está cuantizada y a partir de ahí nos va explicando un poco todo lo que ocurrió después, pero no de forma cronológica, sino didáctica (para que no nos perdamos). Va dando detalles de todo y haciendo énfasis en algunas cosas como que los electrones no tienen una posición definida antes de realizar una medida (no es que la tuvieran y nosotros la ignorásemos, es que no la tenían). Y de ahí explica el experimento de la doble rendija de Thomas Young y la dualidad onda-corpúsculo, el principio de incertidumbre de Heisenberg (que en realidad es un teorema, es decir, una consecuencia matemática de los postulados de la teoría), el interferómetro Mach-Zehnder (y la elección retardada), el teorema de Bell (la desigualdad), la decoherencia (podemos decir que es la interacción de un sistema físico con el entorno, la cual tiene el efecto de degradar la superposición original pura convirtiéndola en una superposición caótica que en la práctica funciona como una mezcla estadística), y el tiempo de decoherencia (tan problemático a la hora de hablar de la computación cuántica), de lo que es una esfera de Bloch, del protocolo BB84 (en criptografía cuántica), del algoritmo de Grover y del de Shor, ...

También dedica un capítulo a las tecnologías cuánticas, para recordarnos que aunque no la entendamos bien, la usamos todos los días cuando vemos cosas como el laser (y comenta lo del espejo que dejaron los astronautas del Apolo 11 en la luna y que nos sirve para medir la distancia con ella mediante un laser), el diodo, el transistor, el GPS ...

En fin, un libro de sólo 333 páginas que se leen muy bien, excepto alguna parte en la que hay algún cero y algún uno (normal cuando se habla de computación), pero que está bien explicado también (salvo un cálculo en la pagina 188 que podría haber desarrollado un poco antes de dar la solución, aunque fuese en un apéndice). Por lo demás, un libro totalmente recomendable.

Como siempre. copio un trocito:

"Por supuesto, tanto los superordenadores como los ordenadores cuánticos son cada vez más potentes, pero esta carrera no pueden ganarla los ordenadores clásicos. Imaginemos que el proceso de miniaturización al que nos tiene acostumbrado la industria informática alcanza su límite físico, que sería almacenar un bit en cada átomo de silicio. El silicio es un elemento muy abundante, el segundo más abundante en la corteza terrestre (después del oxígeno), y representa el 20% de esta. Si consideramos la corteza terrestre hasta una profundidad de 20 kilómetros, resulta que hay unos 4 trillones de toneladas de silicio en ella, que contienen 4 septillones de átomos (un septillón es un 1 seguido de 42 ceros). Esos serían los bits almacenados por este superordenador supremo. Pues bien, esa capacidad de almacenamiento es igualada por un ordenador cuántico de 143 qbits. ¡No estamos tan lejos! Esta es la magia del crecimiento exponencial. Un ordenador de 273 qbits tendrá más memoria que átomos tiene el universo observable".

Clasificación:

Facilidad de lectura: 1-2

Opinión:4 

La zorra y las uvas

 

Escrito por Sean Carroll y publicado en 2020 por Ediciones de Pasado y Presente S.L. (aunque el original en inglés es del 2019). 

A Sean Carroll (no confundir con Lewis Carroll) ya lo conocía por otros libros (entre otros éste que ya he comentado). Como ya dije entonces, es profesor en el Caltech y doctor por Harvard, así que algo sabe sobre los temas de los que escribe.

Lo primero que hay que decir del libro es que, tal y como indica el subtítulo, trata de los mundos cuánticos y la realidad oculta del universo. Lo de titularlo como "la zorra y las uvas" es como homenaje a una fábula de Esopo en la que en este caso la zorra son los físicos y las uvas la comprensión de la mecánica cuántica. Lo segundo es que, tal y como indica el autor, el libro tiene tres mensajes relevantes. El primero es que la mecánica cuántica tiene que ser comprensible (aunque no lo hayamos logrado todavía). El segundo es que hemos conseguido avances reales hacia esta comprensión. Y el tercero es que todo esto es importante, y no solo para la integridad de la ciencia. 

El enigma que yace en el corazón de la mecánica cuántica se puede resumir en un lema bien sencillo: lo que vemos cuando observamos el mundo parece ser esencialmente diferente de lo que es (y ésto son palabras del autor, no mías). Y sobre esto trata el libro, sobre los avances que hemos hecho en nuestro intento de explicar los fundamentos de la mecánica cuántica (no solo el famoso "calla y calcula").

Por supuesto empieza presentándonos a la ecuación de Schrödinger (no puedo evitarlo, la pongo aquí): 

Y las diferentes interpretaciones que de ella han hecho los físicos, entre otras y fundamentalmente la de los muchos mundos de Everett, de la que el autor se manifiesta públicamente defensor (y argumenta los motivos). Como ya ocurrió en el anterior libro que leí de él, a medida que vamos avanzando en el libro, la complejidad se va acumulando (aunque no hay prácticamente ninguna fórmula) y nos habla de modelos de colapso dinámico (como la teoría GRW), de los enfoques epistémicos y ontológicos de la mecánica cuántica, del bayesianismo cuántico, del qbismo, del teorema de Reeh-Schlieder (que viene a decir que al hurgar en un campo cuántico  es posible cambiar el estado cuántico de todo el universo a otro estado), del enigma de la información en un agujero negro (sobre esto comenté algunos libros con anterioridad, entre otros: éste), de la radiación Hawking, de los diagramas de Feynman, de la gravedad entrópica o gravedad termodinámica, etc ...

Vamos, que hay conceptos muy complejos (aunque bien explicados). Otra cosa es que los tengamos todos claros en la cabeza mientras leemos, pero eso no es culpa del autor, si ocurre será culpa nuestra. No obstante, al estar bien escrito, va intercalando cosas que hacen la lectura amena, como cuando cuenta la anécdota de que el hijo de Everett (recordemos que Hugh Everett murió de un infarto a los 51 años) dice que al principio estaba enfadado con su padre por no haberse cuidado más, pero que luego cambió de opinión: "me he dado cuenta de que el estilo de vida de mi padre tiene cierto valor. Comía, bebía y fumaba todo lo que quería, hasta que un día, de golpe, murió rápidamente. Teniendo en cuenta algunas de las otras opciones que he presenciado, tal vez disfrutar y luego morir con rapidez no sea una mala forma de irse". Y también hace un alegato a favor de que otros intenten desarrollar ideas con las que no estamos de acuerdo porque "esto nos brinda la oportunidad de mantener con vida diversas ideas, maximizando así la probabilidad de que lleguemos a la solución correcta".

Por resumir, un libro de 300 páginas que hay que leer con tranquilidad para ir absorbiendo los conceptos sin atragantarnos, pero que merece la pena leer. Esta vez voy a copiar dos trocitos, porque no me decidía sobre ninguno de ellos:

"Los agujeros negros tienen una propiedad muy especial: representan los estados de mayor entropía que podemos tener en una región cualquiera del espacio. Este resultado, sin duda provocador, fue advertido por primera vez por Bekenstein y luego perfeccionado por Raphael Busso. Si consideras una región en el estado de vacío e intentas aumentar su entropía, también debes incrementar su energía (como partimos del vacío, la energía no tiene más remedio que aumentar). A medida que vas añadiendo entropía, la energía también aumenta. Al final tendrás tanta energía en una región limitada que ésta no tendrá más remedio que colapsar para formar un agujero negro. Y aquí nos topamos con el límite; no puedes meter más entropía en una región que la que tendrías si esa región fuera un agujero negro."

"Hay que ser conservador en el sentido de que deberíamos partir de teorías y principios que ya están bien establecidos y tienen éxito, en lugar de introducir de forma arbitraria nuevos enfoques cada vez que se descubren nuevos fenómenos. Pero, a la vez, hay que ser radical, en el sentido de que hay que tomar en serio las predicciones e implicaciones de nuestras teorías en regímenes que están alejados de aquellos en los que se han comprobado".

Clasificación:

Facilidad de lectura: 3

Opinión: 4 (muy bueno, pero para leer con tranquilidad y sin ruido)

Universos paralelos

Escrito por Michio Kaku y publicado por Ediciones Atalanta en 2008 (el original es del 2005).

Del autor ya he comentado otros libros con anterioridad: 1, 2, 3, 4, y 5. Vamos, que ya lo conocía. Es un gran divulgador científico (con programas en la televisión y en la radio, no sólo con libros) y suele escribir de forma muy sencilla para que lo entienda todo el mundo. Por si a alguno no le suena, sólo diré que es un físico teórico (especialista en teoría de cuerdas) y que ha sido profesor visitante en el Instituto de Estudios Avanzados de la Universidad de Princeton.

En este libro hace un recorrido por las ramas más actuales de la cosmología, llegando hasta los límites de la misma y especulando con los posibles futuros de nuestro universo (siempre dentro de lo que se supone que es el espíritu científico, sin pasarse y con una base científica adecuada).

Empieza el libro casi, casi, cuando según Lev Landau: "los cosmólogos se equivocan a menudo pero nunca dudan" (eran los años en los que "hay especulación, después más especulación y después está la cosmología"). Comenta que los "Principia" de Newton se publicaron gracias a Edmund Halley, un rico astrónomo aficionado (sí, el del cometa). Y menciona las diferentes paradojas, como la de Bentley y la de Olbers, y las provocadas por la relatividad, como la de Lorenz-FitzGerald, así como las dificultades con que se fueron encontrando los físicos mientras desarrollaban nuestro actual sistema de "creencias cosmológicas" (como el problema del monopolo, del universo plano y el del horizonte). Habla de los puentes Einstein-Rosen y especula un poco con su posible utilización como vía para los viajes en el tiempo (menciona la paradoja de Fermi y comenta que, quizá, la razón por la que no nos acechan los turistas del futuro es que el tiempo más antiguo al que pueden volver es el momento en el que se creó la máquina del tiempo). Menciona la ecuación de Wheeler-DeWitt, la ecuación de Poisson-Laplace, habla de los distintos tipos de civilizaciones según el consumo de energía (que ya menciona en algún otro libro suyo), de la inflación,  del multiverso, de la teoría de cuerdas (y de las p-branas). Narra el comienzo de la teoría de cuerdas y su relación con la función Beta de Euler y como está relacionándose la moderna teoría de cuerdas (M) con la fuerza de la gravedad en búsqueda de una teoría del Todo (a este respecto menciona una frase de Ken Crowell: "siempre que la inteligencia de la gente aumente con mayor rapidez que el brillo del Sol, la Tierra prosperará").

Nuevamente aparece mencionada la serie de libros de "La guía del autoestopista galáctico" y menciona el motor de impulso de improbabilidad absoluta (como curiosidad), también menciona el libro de Martin Rees: "Seis números nada más".

Resumiendo, un libro que el autor divide en tres partes, una primera en la que habla del Universo, una segunda en la que habla del Multiverso y una tercera en la que habla del Hiperespacio. Son 405 páginas más un glosario final (para la gente que se despista un poco). Se lee de forma muy rápida y como viene siendo habitual con este autor, está escrito de forma asequible para todo el mundo.

Como siempre, copio un trocito:
"Así pues, los postulados de la escuela de Copenhague de Bohr, hablando en términos generales, pueden resumirse del siguiente modo:
a. Toda la energía discurre en paquetes discretos llamados "cuantos" (el cuanto de luz, por ejemplo, es el fotón. Los cuantos de la interacción débil se llaman bosones W y Z, el cuanto de la interacción fuerte se llama gluón, y el cuanto de la gravedad se llama gravitón, algo que todavía no se ha visto en el laboratorio).
b. La materia está representada por partículas puntuales, pero la probabilidad de encontrarse la partícula la da una onda. La onda, a su vez, obedece a una ecuación de onda específica (como la ecuación de Schrödinger).
c. Antes de realizar una observación, un objeto existe en todos los estados posibles simultáneamente. Para determinar en qué estado está el objeto, tenemos que hacer una observación, que "colapsa" la función de onda, y el objeto entra en un estado definido. El acto de observación destruye la función de onda y entonces el objeto asume una realidad definida. La función de onda ha cumplido su propósito: nos ha dado la probabilidad precisa de encontrar el objeto en este estado particular".

Clasificación:
Facilidad de lectura: 1-2
Opinión: 4-5

Fórmulas elegantes

Escrito por Graham Farmelo y publicado por Tusquets editores dentro de la colección Metatemas en 2004 (yo tengo una segunda edición del 2005 y el original es del 2002).

Del autor, decir que, nuevamente, no lo conocía, pero que es director de comunicación científica del Museo de Ciencias de Londres y profesor de física en la Northeastern University, y con eso, hay que darle un poco de crédito. Además, no es un libro escrito por él propiamente dicho, si no, elaborado y diseñado por él, pero compuesto de 11 capítulos, cada uno escrito por un autor distinto (uno por él) y un epílogo de Steven Weinberg (del que acabo de comentar un libro suyo: éste). Vamos, que había que echarle un ojo, sí o sí.

Dado que está desarrollado por capítulos individuales, voy a nombrar cada uno:

• La ecuación de Planck-Einstein (escrito por Graham Farmelo), en el que hace un resumen de la historia de E=hf, incluyendo todos los años que ha estado desentrañándose su significado real. También salen a colación la masa de Planck=√(hc/G), la longitud de Planck=√(hG/c³) y el tiempo de Planck=√(hG/c⁵).
• E=mc² (escrito por Peter Galison). Detalla también la historia de su descubrimiento y su significado. Hay una buena indicación que merece la pena comentar y es que "respetando siempre las leyes de conservación, la energía también puede convertirse en masa".
• La ecuación de la relatividad general (escrito por Roger Penrose). Como no podía ser de otro modo, este es uno de los capítulos más técnicos y nos introduce en la historia y el significado de la famosa fórmula de la relatividad general: R_ab – ½ R g_ab = -8𝜋GT_ab (que relaciona la curvatura del espacio tiempo (lado izquierdo) con la distribución de masa en el universo (lado derecho)) y, aunque parece una ecuación muy sencilla, es una ecuación tensorial (y engaña). Obviamente, nos comenta muchas más cosas, como el principio de equivalencia, las fuerzas de marea, la desviación geodésica, el tensor de curvatura de Riemann (que en el espacio-tiempo tetradimensional tiene veinte componentes), la geometría minkowskiana (que tiene la curiosa propiedad de que la distancia entre dos puntos puede ser nula aunque tales puntos no coincidan), las ondas gravitatorias, el cálculo 2-espínor ...
• La ecuación de Schrödinger (escrito por Arthur I. Miller): Esta es una de mis ecuaciones favoritas y nuevamente, es una que engaña, porque su formulación es muy sencilla, pero la ecuación en sí no lo es tanto. Por supuesto, al narrarnos la historia, menciona también el cálculo matricial de Heisenberg y su equivalencia.
• La ecuación de Dirac (escrito por Frank Wilczek). Esta no engaña tanto, su formulación es algo más compleja, pero encima hay que tener cuidado que es una ecuación matricial.
• Las ecuaciones de Shannon (escrito por Igor Aleksander), que son el pilar de la moderna teoría de la información. Y son muy sencillas las dos: I=-plog₂p, C=Wlog₂(1+S/N). De estas ecuaciones se deduce un principio muy importante que es que "la información es proporcional a lo que desconocemos". Comenta también el método matemático de reducción al absurdo (para validar A, se asume el opuesto de A y se llega a una contradicción (que es la forma más habitual de demostrar que la raíz de dos es irracional)).
• La ecuación de Yang-Mills (escrito por Christine Sutton), que es la ecuación del movimiento del campo de Yang-Mills. Es una ecuación que implica conocimientos bastante altos de física (entre otros de simetrías gauge). Menciona que Emmy Noether constató que cada magnitud que se conserva lleva aparejada una simetría, y viceversa.
• La ecuación de Drake (escrito por Oliver Morton), que nos indica de forma "aproximada" la posibilidad de detectar vida fuera del planeta Tierra. Es un capitulo muy entretenido y en el que mencionan la "autodestrucción genética de la razón" (es decir, la reproducción ilimitada de los imbéciles, y que es la base para una película muy tonta que se llama Idiocracy y que cuando la vi me pareció una exageración y según pasa el tiempo, cada vez creo que se parece más a un documental).
• Las ecuaciones de la vida (escrito por John Maynard Smith). Donde nos habla de la teoría del juego evolutivo y del coste-beneficio, y de la aplicación de métodos matemáticos a la biología.
• El mapa logístico (escrito por Robert May), que es la iteración del siguiente algoritmo: Xsiguiente = a Xinicial (1- Xinicial). Y donde observamos que, dependiendo del valor de "a" podemos encontrarnos con que una ecuación sencilla nos puede llevar a resultados caóticos. En este capitulo recomienda un libro que he aprovechado para comprarme: "Caos: la creación de una ciencia" de James Gleick.
• Las ecuaciones de Molina-Rowland (escrito por Aisling Irwin). Estas las desconocía, y son las que detallan el proceso de descomposición en la atmósfera de los CFC (el agujero de ozono). En realidad la descomposición es un proceso muy sencillo que se puede resumir en que el Cl ataca al ozono: Cl + O3 = ClO + O2 y después ClO + O = Cl + O2 (y volvemos a tener el Cl libre que vuelve a repetir el proceso, eliminando miles de moléculas de O3 (ozono).

Resumiendo, un libro muy interesante, de 356 páginas, que se lee muy bien (algunas partes con algo de atención) y que realmente merece la pena.

Como siempre, copio un trocito:

"Habría que esperar hasta finales del siglo XIX, fecha en la que el caos fue vislumbrado por primera vez por el gran matemático francés Henri Poincaré, al estudiar ciertas ecuaciones diferenciales. A finales del siglo XIX, el rey Oscar II de Suecia ofreció un premio a la primera persona que pudiera demostrar que el sistema solar en su conjunto (el Sol, los planetas, los asteroides, etc ...) era totalmente estable. Fue al intentar conseguir este premio cuando Poincaré abordó el "problema de los tres cuerpos": tres objetos que interaccionan gravitatoriamente (p.ej., el Sol, la Tierra y la Luna), tratados de forma simplificada como si fueran tres puntos. Poincaré demostró que el sistema de ecuaciones diferenciales resultante podía dar lugar a órbitas de "indescriptible complejidad" y concluyó que el problema planteado por el rey era irresoluble, al menos mediante las técnicas disponibles entonces. Tenía razón y, además, fue el primero en entrever el caos, aunque pocos se dieran cuenta en aquel momento. En cualquier caso y para su satisfacción, fue el ganador del premio".

Clasificación:

Facilidad de lectura 3-4 (hay partes un poco complicadas, pero es que habla de ecuaciones muy, muy complejas).

Opinión: 4

El Universo en una cáscara de nuez

Escrito por Stephen Hawking y editado por Editorial Crítica en 2002, aunque el original es de 2001.

Tengo que decir que la edición que tengo es una edición de lujo, que casi da pena leerla por si se arruga alguna hoja, pero había que leerlo y es lo que he hecho. Aún así, todavía tengo algunos libros de este maravilloso científico y divulgador. Uno de ellos: "Breves respuestas a las grandes preguntas" me lo estoy reservando para poder leerme algo de él dentro de unos años.

En principio, el libro viene a ser una continuación del que escribió en 1988, "Historia del tiempo" (que, por cierto, fue el segundo libro de divulgación científica que me leí), pero realmente es una continuación en la que no hace falta haberse leído el primer libro. Como era habitual en él, utiliza un lenguaje muy poco técnico y hace asequible que se entiendan conceptos que son técnicamente muy complejos.

Divide el libro en siete capítulos, bastante independientes unos de otros. En el primero hace un resumen de la relatividad (las leyes de la naturaleza deberían tener el mismo aspecto para todos los observadores que se movieran libremente). En el segundo intenta explicar lo que es el tiempo (y comenta que, si adoptamos la perspectiva positivista, como él hace, no podemos decir qué es realmente el tiempo). En este capítulo aparecen otra vez los campos de Yang-Mills y las dimensiones de Grassmann, menciona a Paul Townsend (p-branas), aparece (en la página 63) la fórmula de la entropía de un agujero negro.
En el tercero habla del espacio que ocupa el universo (de ahí el título del libro: "podría estar encerrado en una cáscara de nuez y sentirme rey de un espacio infinito" (Hamlet) y dice una frase muy buena: "una ley no es una ley si sólo se cumple a veces". En el cuarto intenta predecir el futuro del universo y aparece la ecuación de Schrodinger (que da la tasa con que la función de onda cambia con el tiempo. En el quinto habla de los viajes en el tiempo (indica que, incluso si los viajes en el tiempo son imposibles, es importante que lleguemos a comprender por qué es así). En el sexto habla de nuestro futuro como especie (tanto biológica como técnicamente) y en el séptimo habla de los universos membranas y el principio holográfico (la base es que la holografía codifica la información acerca de lo que hay en una región del espacio en una superficie de una dimensión menos).

En resumen, un libro de 201 páginas, con multitud de gráficos y fotografías, que se lee muy rápido (como todos los de Hawking escritos para el gran público) y que realmente merece la pena. Si uno tiene prisa, se lo puede leer en una tarde.

Como siempre, copio un trocito:
"Los modelos de universos membrana son un tema candente de investigación. Son altamente especulativos, pero ofrecen nuevos tipos de comportamiento que pueden ser sometidos a pruebas observacionales y podrían explicar porqué la gravedad parece ser tan débil. Podría ser que en la teoría fundamental la gravedad fuera muy fuerte, pero que su diseminación en las dimensiones adicionales nos la hiciera parecer débil a distancias suficientemente grandes en la membrana en la que vivimos.
Una consecuencia de ello sería que la longitud de Planck, la distancia más corta a la cual podemos sondear sin producir un agujero negro, sería mucho mayor de lo que se sigue de la debilidad de la gravedad en nuestra membrana cuadrimensional".

Clasificación:
Facilidad de lectura: 1-2.
Opinión: 4 (muy bueno)

Ahora

Escrito por Richard A. Muller y publicado en 2016 por Ediciones de Pasado y Presente S.L.

Sobre el escritor (que yo personalmente no conocía) comentar que es profesor de física en la Universidad de Berkeley y un gran físico experimental. El título del libro y, sobre todo, el subtitulo: "la física del tiempo" deja bastante claro de lo que va a tratar el mismo, que no es otra cosa que lo que se entiende en física por "ahora" y la famosa flecha del tiempo (de la cual se habla en muchos de los libros más famosos de divulgación científica, aunque este es un libro dedicado "sólo" a eso). Es verdad que para lograr entender un poco lo que es el tiempo, habla de gran cantidad de temas, pero podemos reducirlos fundamentalmente de dos: la relatividad y la física cuántica.

Si bien es cierto que no utiliza muchas fórmulas, tampoco es menos cierto que no es de los que sólo ponen la más conocida de Einstein, también pone la de la relatividad general, G=kT, explicando de una forma sencilla lo que es cada una de los tres letras que aparecen en ella, la de la entropía, E=klogW (que ya he hablado de ella en distintos comentarios y que explica también de forma bastante clara diferenciando claramente entre entropía local y global), la fórmula de Plank (E=hf), la de la incertidumbre de Heisenberg ΔxΔp>=h/4PI (y comenta su similitud con la ecuación que describe las ondas clásicas). Y unas cuantas más, pero todas muy bien explicadas, incluso de una forma histórica.

Pero como no todo pueden ser fórmulas (porque sino sería un libro de texto) nos comenta cómo se ha ido pensando sobre el tiempo a través de los años y las diferentes formas de entenderlo. Explica diferentes flechas del tiempo como son: la flecha de la disminución de la entropía, la flecha de los agujeros negros, la flecha de la radiación, la flecha psicológica, la flecha antrópica, la flecha cuántica y la flecha cosmológica (con sólo ver la cantidad de flechas que hay para intentar entender la flecha del tiempo deberíamos darnos cuenta de que el asunto es más complicado de lo que podría parecer a simple vista).

Realmente, a lo largo del libro, y para llegar a las conclusiones finales de una forma que todos podamos opinar, explica un poco de todo, como que al principio ninguna partícula tenía masa y que al evolucionar el universo la adquirieron (a través del mecanismo de Higgs mediante un proceso que se llama ruptura espontánea de la simetría), la posibilidad de la existencia de "agujeros blancos" (un agujero negro invertido en el tiempo), que la reversión del tiempo no es una simetría perfecta de las leyes físicas (i.e., que el tiempo que va hacia adelante es distinto del que va hacia atrás), la interpretación de Copenhague de la física cuántica (i.e., que el famoso gato de Schrodinger está muerto y vivo hasta el momento de la medición, y lo que se entiende por medición), el teorema de Godel (por resumir: todas las teorías matemáticas son incompletas (sobre este asunto comenté otro libro)), la importancia que tiene en física que "si algo no es medible no es real" y de "que si algo no se puede refutar entonces no es ciencia" y, cómo no, vuelve a aparecer Emmy Noether. En fin, multitud de conceptos bastante bien explicados, incluyendo una muy buena forma de entender el concepto que da título al libro: "Ahora es ese momento especial del tiempo que acaba de ser creado en la expansión del universo en dimensión cuatro, como parte de la continuidad del Big Bang en cuatro dimensiones".

Por resumir, un libro de 294 páginas que se leen más o menos bien (en algunas partes hay que concentrarse un poco), con 6 apéndices cortitos que merece la pena leer también (uno de ellos con algo de matemáticas de la relatividad por si a alguien le interesa entrar un poco más en detalles).

Como siempre, copio un trocito:
"Einstein logró dar con una ecuación en la que la geometría del espacio-tiempo quedaba determinada por su contenido en energía. En este enfoque, la fuerza gravitatoria no existe. La presencia de masa significa la presencia de energía; la presencia de energía distorsiona el espacio y el tiempo; la distorsión del espacio y el tiempo conlleva que los objetos parecen responder a fuerzas gravitatorias, cuando de hecho sólo se guían por el instinto (i.e., se mueven rectos hacia adelante) a través de un complicado espacio-tiempo curvo. En su jerga, los planetas que orbitan alrededor de una estrella se mueven en realidad en línea recta, una línea recta no a través del espacio, sino del espacio-tiempo."

Clasificación:
Facilidad de lectura: 2-3
Opinión: 4 (está bastante interesante y lleno de conceptos muy bien explicados).

Cuántica

Escrita por Jim Al-Khalili en 2003 y publicada por Alianza Editorial en 2016, que es cuando me han regalado el libro a mi y he podido leerlo.

Bueno, el título hay que reconocer que llama la atención y lo de "guía para perplejos" (osea, todos) también. Y entre eso y el echar un vistazo en internet a ver quién es el autor y comprobar que es profesor de física en la Universidad de Surrey en UK y que tiene alguna charla interesante en TED, merecía la pena hacer el intento de leer el libro (nunca se sabe si uno va a estar a la altura de entender lo que el cuentan, pero que no se diga que no se intenta).

El libro lo que pretende es dejar al lector con una idea más o menos clara (dentro de lo claras que puede tener uno las ideas en este tema) de lo que es la mecánica cuántica, de para qué se usan sus efectos y propiedades en la actualidad, por muy extrañas que parezcan, y de sus posibles usos futuros. De esta forma no tenemos por qué creernos todo lo que nos dicen, podemos comprobar con actuales usos de lo que nos están contando, que las cosas, aunque sean raras, son como son. De hecho, son tan raras que él mismo reconoce que entre los físicos que se dedican a trabajar con la mecánica cuántica hay un dicho que es: "no pienses y calcula" que viene a hacer referencia a que si uno empieza a pensar mucho sobre el significado de lo que está haciendo, es muy probable que no termine de hacer nada. El autor se reconoce más partidario de "calcular cuando ya no está pensando", que viene a ser otra forma de hacer lo mismo pero de forma diferente. Sobre este tema, en alguno de los libros que me he leído, aparece detallada una anécdota entre dos físicos que se encuentran y le pregunta uno al otro sobre qué está haciendo un alumno suyo que parecía tan brillante y el otro responde: "nada, está intentando encontrar el sentido a la mecánica cuántica y se ha quedado atascado sin llegar a ningún sitio". En fin, que trabajar con ecuaciones que funcionan no quiere decir que entendamos realmente lo que nos quieren decir (aunque no por ello hay que dejar de intentar pensar sobre el asunto).

Como no podía ser de otra forma, empieza con el famoso experimento de la doble rendija del que da bastantes explicaciones distintas, para que se entienda de verdad la repercusión que tiene el resultado que se obtiene dependiendo de si se realizan mediciones o no. De este experimento ya comenté que en otro libro daban una muy buena explicación (éste). Y según va dando explicaciones, van apareciendo conceptos, propiedades y situaciones nuevas, como la constante de Planck, la ecuación de Schrödinger (perfectamente explicada en la página 88 y que no puede evitar escribir al comentar otro libro: éste), la superposición, la paradoja EPR y la ecuación de Bell (que ya comenté en otro libro: éste), la decoherencia (sobre este tema hicieron una película bastante curiosa, Coherence, y al final copiaré un trocito que explica un poco el concepto), y multitud de conceptos e ideas nuevas incluida la computación cuántica, el caos cuántico, la gravitación cuántica, etc ... y alguna referencia final al cerebro cuántico (tal y como se refería a él Sir Roger Penrose en otro libro comentado con anterioridad: éste). Y tal y como ya he indicado, nos habla de aparatos actuales que utilizan las extrañas propiedades cuánticas para obtener resultados sorprendentemente útiles, como los SEM (microscopio electrónico de barrido), los STM (microscopio de efecto túnel), los SQUID (superconducting quantum interference device), las RMN (resonancia magnética nuclear) y algunos más, y nos da una buena explicación de la base de su funcionamiento.

En fin, un buen libro, con algunas partes en las que hay que centrarse para no perderse (normal cuando se habla de estos temas) pero que está bastante bien escrito y explicado. Una lectura recomendable de 375 páginas y un par de páginas finales con lecturas que nos recomiendo el autor (alguna de ellas ya comentada en este blog).

Como siempre, copio un trocito:

"La decoherencia es un proceso físico real que ocurre en todas partes en todo momento. Se produce siempre que un sistema cuántico deja de estar aislado de su entorno macroscópico circundante y su función de onda se entrelaza con el complejo estado de su entorno. Puede pasar con cualquier cosas, desde una pantalla fotosensible o un dispositivo electrónico hasta las moléculas del aire de alrededor. Si el acoplamiento a ese entorno "exterior" es lo bastante intenso, entonces la delicada superposición inicial se pierde con rapidez. De hecho, la decoherencia es uno de los procesos más veloces y eficaces de toda la física, y es precisamente esa enorme eficacia la responsable de que se haya tardado tanto en descubrirla; es ahora cuando los físicos están aprendiendo a controlarla y estudiarla.

En física se dice técnicamente que la función de onda del entorno pierde todos los restos de las correlaciones de la fase inicial entre sus dos partes entrelazadas. Para expresarlo de una manera más animada bastaría con decir que cuando una superposición cuántica se entrelaza con el mundo exterior, desaparece toda la rareza y se pierde tan deprisa que nunca llegamos a verla en acción."

Clasificación:

Facilidad de lectura: 3 (hay partes en las que hay que concentrarse).

Opinión: 4.

La realidad cuántica

Escrito por Andrés Cassinello y José Luis Sánchez Gómez y publicado por Editorial Crítica dentro de la colección Drakontos en 2012.

Los autores son doctores en Física, uno de ellos, catedrático de física teórica en la UAM, y aunque sólo sea por eso, había que leer el libro. Bueno, por eso y por pertenecer a la magnífica serie de libros que para mi es la colección Drakontos (de la que ya he comentado bastantes libros y seguiré haciéndolo, que tengo unos cuantos más pendientes de leer).

Como ya nos indican nada más empezar, el objetivo del libro es explicar los fundamentos de la mecánica cuántica y sus aplicaciones recientes. Pero ojo, que también avisan: la mecánica cuántica nadie la entiende, así que lo que pretenden explicar es qué se sabe y de qué manera.

Comienzan con un primer capítulo en el que explican un poco el átomo de Bohr, las líneas espectrales y la función "psi" de la ecuación de ondas de Schrödinger (de la cual hablé un poco y puse la fórmula en el comentario de otro libro: "17 ecuaciones que cambiaron el mundo"), que expresa la probabilidad de que una partícula se encuentre en un sitio u otro. Para concluir el capítulo con algunos detalles de la vida de Schrödinger y del estilo de vida en la Viena de principios de 1900. En el segundo capítulo intentan dilucidar el significado de la "función de onda" y nos introduce en las dos reglas básicas de la mecánica cuántica: "Superposición: si hay dos (o más) alternativas indistinguibles de llegar a un resultado, la función de onda será la superposición de las funciones de onda de las diferentes posibilidades. Colapso: en cuanto hay manera de distinguir cuál de las alternativas puede darse, la función de onda colapsa". Y para que entendamos bien este concepto, explica (de forma muy clara) el experimento del interferómetro de Mach-Zehnder, y cómo los fotones se comportan unas veces como partículas y otras como ondas. También nos dan una breve explicación de la interpretación de Copenhague de la mecánica cuántica. Los capítulos tres y cuatro los dedican a explicar qué se entiende por medida (a nivel cuántico) y qué entendemos por entrelazamiento. En ellos da una definición original (al menos para mi) de lo que son los fermiones y bosones (las partículas que, cuando se intercambian, hacen que la función de onda cambie de signo se llaman fermiones, las que, en cambio, cuando se intercambian, dejan la función de onda inalterada, manteniendo también el signo, se llaman bosones). El capítulo cinco está íntegramente dedicado a la desigualdad de Bell, aunque para la explicación utilizan una versión más simple que es la desigualdad CHSH (la explican también en el link anterior). Explican la desigualdad de forma bastante clara, pero hay que prestar atención, que, para hacernos una idea, la desigualdad de Bell es de 1964 y la complejidad de los experimentos para su demostración era tal que el primero se llevó a cabo en 1982. La consecuencia de la comprobación experimental de la violación de la desigualdad es muy clara: "las magnitudes permanecen en estado de indefinición hasta que las observamos, las medimos. Tenemos que aceptar que el mundo es radicalmente aleatorio".

Una vez que tenemos las herramientas para "entender" un poco cómo funciona la mecánica cuántica, en el capitulo seis entran en lo que se entiende por "información cuántica" (o teoría cuántica de la información) y en asuntos tales como computación cuántica (qbits), criptografía y teleportación. Dentro de la computación cuántica, hablan de los logros de Ignacio Cirac y sus trampas de iones, nos introducen al concepto de "decoherencia", que es el nombre que recibe la pérdida de superposición por el acoplamiento con un entorno con muchos grados de libertad, y mencionan y explican un poco cómo se entrelazaron tres partículas en un estado de superposición que desde entonces vino a llamarse estado GHZ con el que en 1999 logró demostrarse, sin necesidad de cálculos estadísticos, la violación de la desigualdad de Bell. En el capitulo siete nos hablan de la criptografía y de lo que se entiende por criptografía cuántica, que amenaza seriamente el algoritmo más usado hoy en día que es el RSA (del que por cierto da un magnífico ejemplo en las páginas 152 y 153).

Para finalizar, dan un repaso a las aplicaciones, a nivel general de la física, que está teniendo la mecánica cuántica, por ejemplo con el tema de la información que se conserva en los agujeros negros (de este tema comenté algo en cuando hablé del libro: "La guerra de los agujeros negros"), y, como no podía ser de otra manera, vuelve a aparecer la fórmula de la entropía.

Luego hay un par de nexos con algunos detalles técnicos, pero se puede decir que el libro se lee bastante bien y no tiene una complejidad narrativa excesiva, aunque en algunos momentos hay detalles de desarrollos de fórmulas, que si alguien no puede seguir, no pasa nada porque se puede ir a las conclusiones que se sacan de esos desarrollos. A fin de cuentas nadie nos va a examinar y lo importante es ver que los conceptos de los que se habla no son mágicos y se deben a desarrollos matemáticos correctos. Por resumir, 200 páginas que se leen bastante bien.

Como siempre, copio un trozo:
"Para entender por qué la teoría de cuerdas puede "salvar" el principio cuántico de conservación de la información en la caída en un agujero negro, necesitamos la idea de entropía de un agujero negro. Ésta fue introducida por Jacob Bekenstein en 1973, al estudiar - teóricamente - ciertas propiedades de los agujeros negros. En particular, analizó la observación de Hawking acerca de lo que ocurría en una hipotética colisión de dos de ellos, en la que el científico hizo notar que - según la teoría - la superficie total del horizonte de ambos agujeros al entrar en contacto nunca era menor que la suma de las superficies individuales. Como a la entropía le ocurre exactamente lo mismo, es decir, la entropía de un sistema nunca es menor que la suma de la de sus posibles constituyentes, Bekenstein llegó a la audaz conclusión de que la entropía de un agujero negro es proporcional l área de la superficie de su horizonte.

Clasificación
Facilidad de lectura: 2-3 (el tres es si seguimos los desarrollos de las fórmulas).
Opinión: 4 (hace un muy buen resumen de la mecánica cuántica).

17 ecuaciones que cambiaron el mundo

Escrito por Ian Stewart y publicado por Editorial Crítica en 2013.

El escritor es un catedrático de matemáticas en la Universidad de Warwick y un gran divulgador científico. Yo mismo tengo un par de libros suyos en casa pendientes de leerme, entre otros: De aquí al infinito y El laberinto mágico.

El libro, como muy bien indica el título, dedica cada uno de sus 17 capítulos a una ecuación que ha supuesto un cambio en la vida de las personas (aunque en muchas ocasiones ni siquiera nos demos cuenta). 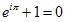Como resumen, lo mejor que puedo hacer es, primero, enumerar los temas (ecuaciones) de los que habla: teorema de Pitágoras, logaritmos, derivadas, Ley de gravitación universal, i (en este capítulo vuelve a aparecer la ecuación de Euler (), que es la ecuación más bonita de todas las matemáticas, al menos en mi opinión, como ya dije al comentar otro libro), Fórmula de Euler para poliedros, distribución normal, ecuación de onda, transformada de Fourier, ecuación Navier-Stokes, ecuaciones de Maxwell, segunda ley de la termodinámica, relatividad, ecuación de Schrödinger, teoría de la información, teoría del caos y ecuación de Black-Scholes.

En la primera hoja de cada capítulo escribe la ecuación de la que va a tratar, indica lo que significa cada símbolo en ella y además comenta los usos principales que hacemos hoy en día de esa ecuación. La verdad es que el desarrollo de los capítulos está muy bien trazado y obliga a pensar en muchos temas distintos. Por ejemplo, a mi nunca se me había ocurrido trazar una historia desde el teorema de Pitágoras hasta la geometría diferencial actual (y las diferentes métricas asociadas). Alguno de los capítulos tengo que reconocer que tienen cierta dificultad conceptual, pero es que es normal que tratando las ecuaciones que trata el asunto se complique en algunos momentos (en la facultad estuve cuatro meses estudiando la resolución de la ecuación de Schrödinger en espacios de Sobolev y aquí la explican en un capitulo de 21 páginas). No puedo resistirme a ponerla (de hecho la llevo escrita en mis aletas de buceo):

Bien, esa es la famosa ecuación de Schrödinger (fundamental en la mecánica cuántica) y en el capítulo 14 la explica bastante bien.

A pesar de eso, la verdad es que merece la pena echarle un vistazo, son 394 páginas (más unas notas finales) que pueden hacerse un poco densas si las leemos todas seguidas, pero como cada capítulo es independiente, se puede leer de semana en semana resultando una lectura bastante agradable (de esas que reactivan el cerebro un poco). Se habla de prácticamente todos los temas físicos (gravedad, relatividad, mecánica cuántica, caos, ...) y matemáticos (álgebra, cálculo, geometría, ...). Dedica un capítulo entero a la teoría de la información de Shannon, que viene muy bien para entender los conceptos de entropía y de información (tan de moda ahora con las nuevas teorías sobre la pérdida o no de información en los agujeros negros). Incluso en el último capítulo, habla de los derivados financieros y el posible origen de la última crisis económica.

Como siempre, copio un trocito:
"Algunas ecuaciones son universalmente válidas. Algunas describen el mundo muy exactamente, pero no perfectamente. Algunas son menos precisas, confinadas a reinos más limitados, aunque ofrecen un entendimiento vital. Algunas son básicamente erróneas sin más, aunque pueden actuar como peldaños hacia algo mejor. Todavía podrían tener un efecto enorme.
Algunas incluso desvelan cuestiones difíciles, de naturaleza filosófica, sobre el mundo en que vivimos y nuestro lugar en él. El problema de las mediciones cuánticas, escenificadas por el desafortunado gato de Schrödinger, es una de ellas. La segunda ley de la termodinámica presenta temas profundos sobre el desorden y la flecha del tiempo. En ambos casos, algunas de las paradojas aparentes pueden ser resueltas, en parte, pensando menos en el contenido de la ecuación y más en el contexto en el que se aplica. No en los símbolos, sino en las condiciones de contorno. La flecha del tiempo no es un problema sobre la entropía; es un problema sobre el contexto en el cual pensamos en la entropía."

Clasificación:
Facilidad de lectura: 2-3 (las ecuaciones no suelen facilitar la lectura)
Opinión: 4 (merece la pena leerlo).