Escrito por Jeremy J. Gray y publicado por Editorial Crítica en 2003 (el original es del 2000) dentro, como no, de su colección Drakontos.
Tengo que volver a reconocer, como ya me ha pasado en otros libros anteriores, que al autor no lo conocía previamente, pero la idea de leerme un libro sobre la conferencia que dio en 1900 Hilbert en París era algo que me atraía bastante (como le debería pasar a casi todos los matemáticos). Para todos aquellos que no hayan oído hablar de David Hilbert, decir que fue uno de los grandes matemáticos de finales del siglo XIX y principio del XX y como muchos de los de aquella época estuvo dando clases en la Universidad de Göttingen. Para los matemáticos y físicos es conocido, sobre todo, por los famosos espacios de Hilbert (un tipo particular de espacios de Banach).
El libro, como indica en el subtitulo: "los 23 problemas que desafiaron a la matemática", trata de la conferencia que dio Hilbert en 1900 en París (la segunda conferencia del ICM, que tuvimos la suerte de celebrar una en 2006 en España). Como muy bien explican, Hilbert se planteó dar una conferencia normal, sobre lo que se había hecho en los últimos años y los avances conseguidos, pero después de pensarlo y hablarlo con Minkowski (sí, el famoso del espaciotiempo de Minkowski) decidió: "... hacer una caracterización de los problemas a los que los matemáticos deberían orientarse en el futuro.", y así lo hizo. Y para ello preparó 23 problemas (aunque no habló de todos ellos durante su conferencia por cuestión de tiempo, pero sí estaban todos en las actas de la conferencia).
Para que vayamos entrando en materia, el libro comienza relatando un poco los avances que logró Hilbert a lo largo de los años anteriores a la conferencia y también sobre la primera conferencia del ICM que dio otro de los grandes de todos los tiempos: Henri Poincaré, del que se dice que fue el último matemático en conocer todas las matemáticas de su época (y que cada vez que oigo su nombre me acuerdo del teorema de Poincaré-Bendixson, será por deformación estudiantil). Nos comenta los estudios de Hilbert sobre geometría no euclídea, teoría de invariantes, teoría de números, ... y como fue decidiendo y seleccionando los problemas que iba a incluir en su conferencia (están todos en el link que he puesto relativo a su conferencia). El libro se adentra un varios de ellos y en si han sido finalmente resueltos o aún no (entre los que aún no han sido resueltos totalmente están la hipótesis del continuo y la hipótesis de Riemann). Y finalmente transcribe la conferencia completa (las actas, con todos los problemas).
Está muy bien narrado, dentro de que los problemas en sí son bastante complejos (por eso los escogió). Pero introduce conceptos curiosos y anécdotas que van haciendo llevaderas las partes más complejas. Por ejemplo, habla del principio de Dirichlet (también conocido como el principio del palomar, que de forma sencilla lo que viene a decir es que "si hay n huecos en un palomar y n+1 palomas, entonces hay al menos un hueco en el que viven al menos dos palomas"), comenta una gran frase de Plutarco: "no se sigue por necesidad que, si la obra te agrada con su gracia, aquel que la forjó sea digno de tu estima", introduce un chiste de matemáticos polacos, en el que un matemático polaco responde a por qué tanto antes como después de la segunda guerra mundial en Polonia habían trabajado sobre algo tan recóndito como la lógica matemática, y el matemático responde: " antes de la guerra lo hacíamos porque la Iglesia no podía entenderlo, y ahora lo hacemos porque el Partido no puede entenderlo" (sobre matemáticas en Polonia, comenté un libro muy bueno sobre la vida de Ulam). Y como no, cuando se habla de lógica, vuelve a salir Gödel (del que ya comenté su famoso teorema en este link).
Por resumir, 258 páginas más 49 de la conferencia, que se pueden leer a ratitos ya que cada problema es medio independiente del anterior y no hay por qué forzar el cerebro más de lo estrictamente necesario.
Copio un trocito:
"La habilidad concreta de Hilbert puede haber residido en su capacidad de ver, o crear, el escenario general correcto que hacía que los problemas viejos y difíciles parecieran fáciles, pero él creó teorías que funcionaban. Quizá haya producido algunos de sus mejores trabajos en algunas de las áreas más puras de las matemáticas, pero también vale la pena recordar que tuvo un persistente interés en la física. Yo diría que Hilbert no planteó 23 problemas. Ni exhortó a la axiomatización y abstracción en un mundo concreto. Exhortó al proceso de equilibrar problemas con teorías y desarrollarlos a la vez. Es en este sentido, como evidenciaban sus 23 problemas, en el que era, como le calificó Blumenthal, un hombre de problemas.".
Clasificación:
Facilidad de lectura: 3-4 (no hay que olvidar que está hablando de problemas de las matemáticas y hay mucha formula por el camino, aunque las evita todo lo que puede).
Opinión: 3-4 (yo diría que un 4 para los científicos y un 3 para el resto).
Para que vayamos entrando en materia, el libro comienza relatando un poco los avances que logró Hilbert a lo largo de los años anteriores a la conferencia y también sobre la primera conferencia del ICM que dio otro de los grandes de todos los tiempos: Henri Poincaré, del que se dice que fue el último matemático en conocer todas las matemáticas de su época (y que cada vez que oigo su nombre me acuerdo del teorema de Poincaré-Bendixson, será por deformación estudiantil). Nos comenta los estudios de Hilbert sobre geometría no euclídea, teoría de invariantes, teoría de números, ... y como fue decidiendo y seleccionando los problemas que iba a incluir en su conferencia (están todos en el link que he puesto relativo a su conferencia). El libro se adentra un varios de ellos y en si han sido finalmente resueltos o aún no (entre los que aún no han sido resueltos totalmente están la hipótesis del continuo y la hipótesis de Riemann). Y finalmente transcribe la conferencia completa (las actas, con todos los problemas).
Está muy bien narrado, dentro de que los problemas en sí son bastante complejos (por eso los escogió). Pero introduce conceptos curiosos y anécdotas que van haciendo llevaderas las partes más complejas. Por ejemplo, habla del principio de Dirichlet (también conocido como el principio del palomar, que de forma sencilla lo que viene a decir es que "si hay n huecos en un palomar y n+1 palomas, entonces hay al menos un hueco en el que viven al menos dos palomas"), comenta una gran frase de Plutarco: "no se sigue por necesidad que, si la obra te agrada con su gracia, aquel que la forjó sea digno de tu estima", introduce un chiste de matemáticos polacos, en el que un matemático polaco responde a por qué tanto antes como después de la segunda guerra mundial en Polonia habían trabajado sobre algo tan recóndito como la lógica matemática, y el matemático responde: " antes de la guerra lo hacíamos porque la Iglesia no podía entenderlo, y ahora lo hacemos porque el Partido no puede entenderlo" (sobre matemáticas en Polonia, comenté un libro muy bueno sobre la vida de Ulam). Y como no, cuando se habla de lógica, vuelve a salir Gödel (del que ya comenté su famoso teorema en este link).
Por resumir, 258 páginas más 49 de la conferencia, que se pueden leer a ratitos ya que cada problema es medio independiente del anterior y no hay por qué forzar el cerebro más de lo estrictamente necesario.
Copio un trocito:
"La habilidad concreta de Hilbert puede haber residido en su capacidad de ver, o crear, el escenario general correcto que hacía que los problemas viejos y difíciles parecieran fáciles, pero él creó teorías que funcionaban. Quizá haya producido algunos de sus mejores trabajos en algunas de las áreas más puras de las matemáticas, pero también vale la pena recordar que tuvo un persistente interés en la física. Yo diría que Hilbert no planteó 23 problemas. Ni exhortó a la axiomatización y abstracción en un mundo concreto. Exhortó al proceso de equilibrar problemas con teorías y desarrollarlos a la vez. Es en este sentido, como evidenciaban sus 23 problemas, en el que era, como le calificó Blumenthal, un hombre de problemas.".
Clasificación:
Facilidad de lectura: 3-4 (no hay que olvidar que está hablando de problemas de las matemáticas y hay mucha formula por el camino, aunque las evita todo lo que puede).
Opinión: 3-4 (yo diría que un 4 para los científicos y un 3 para el resto).









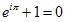 ), que es la ecuación más bonita de todas las matemáticas, al menos en mi opinión, como ya dije al comentar otro
), que es la ecuación más bonita de todas las matemáticas, al menos en mi opinión, como ya dije al comentar otro 